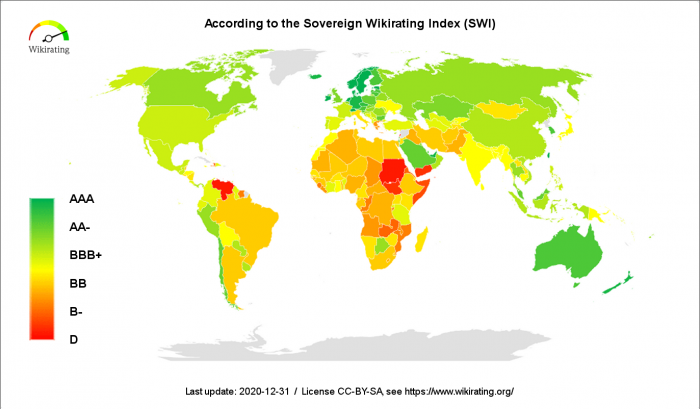
Criteria and Base-Data
The Sovereign Wikirating Index (SWI) is a framework which evaluates the credit rating of sovereign countries/territories based on economic indicators. The following five mid-term and three long-term criteria are used:
- Public debt (in % of the GDP)
- Account balance (in % of the GDP)
- GDP growth rate
- Inflation rate
- Unemployment rate
The resulting value is calibrated by multiplying it with a ‘scaling factor’, which is composed by three long-term indicators, the Human Development Index (HDI), the Corruption Perceptions Index (CPI) and the Economic Freedom Index (EFI). Originally, the third index Political Instability Index was used for the first version of the SWI[1]Unfortunately this index has not been updated since 2010 from “The Economist”, therefore it has been removed as criteria from the SWI, and the ratings for 2011 are retroactively … Continue reading. Each criterium is calibrated with respect to the relative minimum and maximum value of all countries. For some criterion a threshold value is defined in order to avoid distorted values.
| Short Title | Long Title | Value | Weight | Real Min | Real Max | SWI Min | SWI Max |
|---|---|---|---|---|---|---|---|
| HDI | Human Development Index | Weighted index of development indicators | 50% | 0 | 1[2]Raw Data of social scaling factors is divided by the Real Max value to normalize the input. | 0 | 1 |
| CPI | Corruption Perceptions Index | Index of perceived corruption | 30% | 0 | 10[3]Raw Data of social scaling factors is divided by the Real Max value to normalize the input. | 0 | 1 |
| EFI | Economic Freedom Index | Index of economic freedom | 20% | 0 | 10[4]Raw Data of social scaling factors is divided by the Real Max value to normalize the input. | 0 | 1 |
| PII | Political Instability Index | Index of political instability (not used any more)[5]Unfortunately this index has not been updated since 2010 from “The Economist”, therefore it has been removed as criteria from the SWI, and the ratings for 2011 are retroactively … Continue reading | – | 0 | 10[6]Raw Data of social scaling factors is divided by the Real Max value to normalize the input. | 0 | 1 |
| PD | Public Debt | Debt/GDP as %, reflects the economies ability to honour loans. | 40% | 0 | ∞ | 0.2 | 2.0 |
| AB | Current Account Balance | Current account balance as % of GDP, reflects foreign inflows and outflows. | 15% | -∞ | ∞ | -0.2 | 0.2 |
| PG | GDP Growth | Domestic growth an an annual % | 15% | -1 | ∞ | -0.03 | 0.06 |
| IR | Consumer Price Index | Consumer Price index as % | 15% | -1 | ∞ | 0.02 | 0.2 |
| UR | Unemployment Rate | Rate of unemployment as % | 15% | 0 | 1 | 0.02 | 0.3 |
| R | Rating | Result of SWI calculation as % | – | 0 | 1 | 0 | 1 |
Formula
| Definition | Explanation |
|---|---|
Let c be an element in the set of countries C:
| That means that every c is a country. |
Let R be the vector of ratings, so that
| That means that Rc is the rating for the country c and every rating is ranging from 0 to 100%. |
| Let \operatorname{dim}\left(v\right) be the dimension of v | The function \operatorname{dim} basically counts the number of elements in the vector. In example, \operatorname{dim}\left( R \right) is the total number of ratings and thus the number of rated countries. |
| Let \operatorname{min}\left(v\right) the minimal, and \operatorname{max}\left(v\right)the maximal value of v | These functions find the smallest and the biggest number in a set of numbers, such as a vector. This is needed for normalization. |
| \operatorname{norm}(v) = \frac{v-\min(v)}{\max(v)-\min(v)} | We are defining a scale-normalizating function on an vector v. |
| Let \operatorname{B}(x) = {\mathbf C} \times \left\{ \mathrm{HDI, CPI, EFI, PD, AB, PG, IR, UR} \right\} | x is a matrix. We define the base B of this matrix, so that it contains vectors with factors for individual countries in the direction x_c, while the economic and social factors are in direction x^i. |
| Let s\in\left\{\mathrm{HDI,CPI,EFI}\right\} and e\in\left\{\mathrm{PD,AB,PG,IR,UR}\right\} | s is an indexer for the social factors and e is the indexer for economic factors. |
| w^\mathrm{HDI} = 50%, w^\mathrm{CPI} = 30%, w^\mathrm{EFI} = 20%, w^\mathrm{PD} = 40%, w^\mathrm{AB} = 15%, w^\mathrm{PG} = 15%, w^\mathrm{IR} = 10%, w^\mathrm{UR} = 15% | Applying the weights. The vector w^i contains the (scalar) weights for the individual economic and social factors. |
| r = \left( x^s\,w^s \right) \cdot \left( x^e\,w^e \right) | By using the Einstein notation, we weight and sum the social factors to get the scaling factor. We also weight and sum the economic factors. Then we multiply the two results. |
| R = \operatorname{norm}\left(r\right) + \left(1-n \right)\cdot \left( 1-\operatorname{norm}\left(r\right) \right) | We finally do some normalisation on the rating r, so that the resulting values are ranging from 0 to 100% and the values represent the performance relative to the other rated countries. The result of this formula is the SWI rating R. n is a vector that contains the number of given ratings for a specific country and thus the trust in the values. |
Calculation
Download: Sovereign Wikirating Index Framework (Version 2020) – please contact us
General Variable Modifiers
For example, the variable AB.
- AB = Number used in calculations for SWI.
- rAB = Raw or real value, actual data from source in whichever format it is acquired.
- wAB = Weighting value for the data.
- minAB = Floor value of variable, will cause ABC to equal 0 or 100 if ABC is below this value.
- maxAB = Ceiling value of variable, will cause ABC to equal 0 or 100 if ABC is above this variable.
- nAB = Number of ratings (for rating)
So for instance, if the real value (rAB) was 4 on a 10 point scale, this would be divided by 10 to create the value for calculations (AB) which, in calculations, is multiplied by the weighting (e.g. 0.5 for 50% weight.)
List
See also
- Blog article “Outlook 2021 – Wikirating updates 186 Country Ratings.” (01-01-2021)
- Blog article “Wikirating updates 181 Sovereign Credit Ratings” (01-01-2020)
- Human Sustainable Development Index Data (HSDI)[7]See http://www.igbp.net/download/18.20d892f132f30b443080002610/1376383086744/HDI-HSDI_ranks.pdf and https://de.wikipedia.org/wiki/Human_Sustainable_Development_Index
References[+]
| ↑1, ↑5 | Unfortunately this index has not been updated since 2010 from “The Economist”, therefore it has been removed as criteria from the SWI, and the ratings for 2011 are retroactively recalculated. |
|---|---|
| ↑2, ↑3, ↑4, ↑6 | Raw Data of social scaling factors is divided by the Real Max value to normalize the input. |
| ↑7 | See http://www.igbp.net/download/18.20d892f132f30b443080002610/1376383086744/HDI-HSDI_ranks.pdf and https://de.wikipedia.org/wiki/Human_Sustainable_Development_Index |